[10000印刷√] 円錐 の 体積 公式 351086-円錐の体積 公式

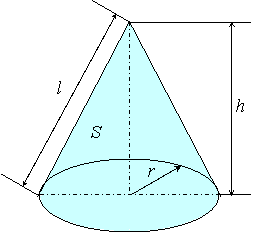
数学の公式集 No 012 幾何図形 円錐の体積と表面積

 円錐は展開図にすると，円と扇形に分離されるのでこのような公式になります． 展開図がそのまま数式になっているので非常に分かりやすく理解しやすいと思います． 体積を求める公式 V = 1 3 π r 2 h V = 1 3 π r 2 h さて，次は円錐の体積を求める公式です 計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく 円錐の表面積 12M views Discover short videos related to 円錐の表面積 on TikTok Watch popular content from the following creators 数スタ(@studyline3), 楽しく勉強あきとんとん(@akitonton), あ(@jpjpwagp), かずおっち(@kazuocci), Tonomura塾長

円錐の体積 公式

円錐の体積 公式-〇〇錐という立体の体積は底面積×高さ×\(\frac{ 1 }{ 3 }\)と覚えている方も多いと思いますが、\(\frac{ 1 }{ 3 }\)という係数はここの導出過程から出てくるものです。 球 最後に球の体積についてです。半径\(R\)の球の体積を求めてみたいと思います。体積の求め方 重量の求め方 体積の求め方 立体 体積v 截頭円柱 角すい 球冠 楕円体 楕円環 交叉円柱 中空円柱（管） 截頭角すい 球分 円環 円すい 球 球帯 樽形 重量の求め方

三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学

 円錐台の体積を求める公式はあるようですが、 楕円錐台の体積を求める公式というのはあるのでしょうか？ また仮に、上面と下面の楕円の面積がわかっているとすれば、 その公式はどのようになりますでしょうか？ 円錐の体積の求め方公式 円錐の体積は、次の公式で求められます。 円錐の体積＝底面積×高さ÷3 円錐の底面積は円の面積ですので、円の面積×高さ÷3で求めることができます。 ⇒ 円の面積の求め方 スポンサードリンク 円錐の体積の求め方の公式って？？ こんにちは、この記事をかいているKenだよ。犬の散歩が趣味だね。 円錐の体積の求め方の公式は、 底面積×高さ×1/3 だったよね。 もう少し詳しくかいてあげると、 半径×半径×円周率×円錐の高さ×1/3 になるんだ。

 まとめ 円錐の高さを求める問題は、ほぼこの2パターン！ 母線と半径から、三平方の定理を使って求める 体積と半径から、円錐の体積の公式を使って求める はかせちゃん 今日もお疲れ様でした～ また会える日を楽しみにしていますね 関連記事は この記事の目的：錐形を求める際に「3分の1」する理由を中学生にも分かるように説明する． はじめに 錐形は3分の1 指針 ①特別な四角錐を考える ②特別な三角錐を考える ③錐体の体積の求め方の根本を考える ④体積が変わると？ 最後に これを公式化すると下のようになります。公式円柱の体積＝底面積×高さ ＝半径×半径×円周率×高さ ＝πr2h ＝Shちなみに円錐の体積を求める公式もあります。詳しくは別の機会に説明できればと思いますが、円錐の体積は底面が同じ形の円柱の1

円錐の体積 公式のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	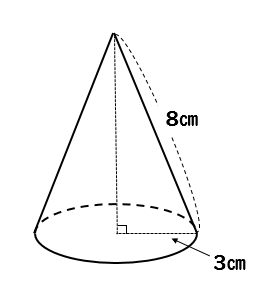1	1
1	1	1
1	1	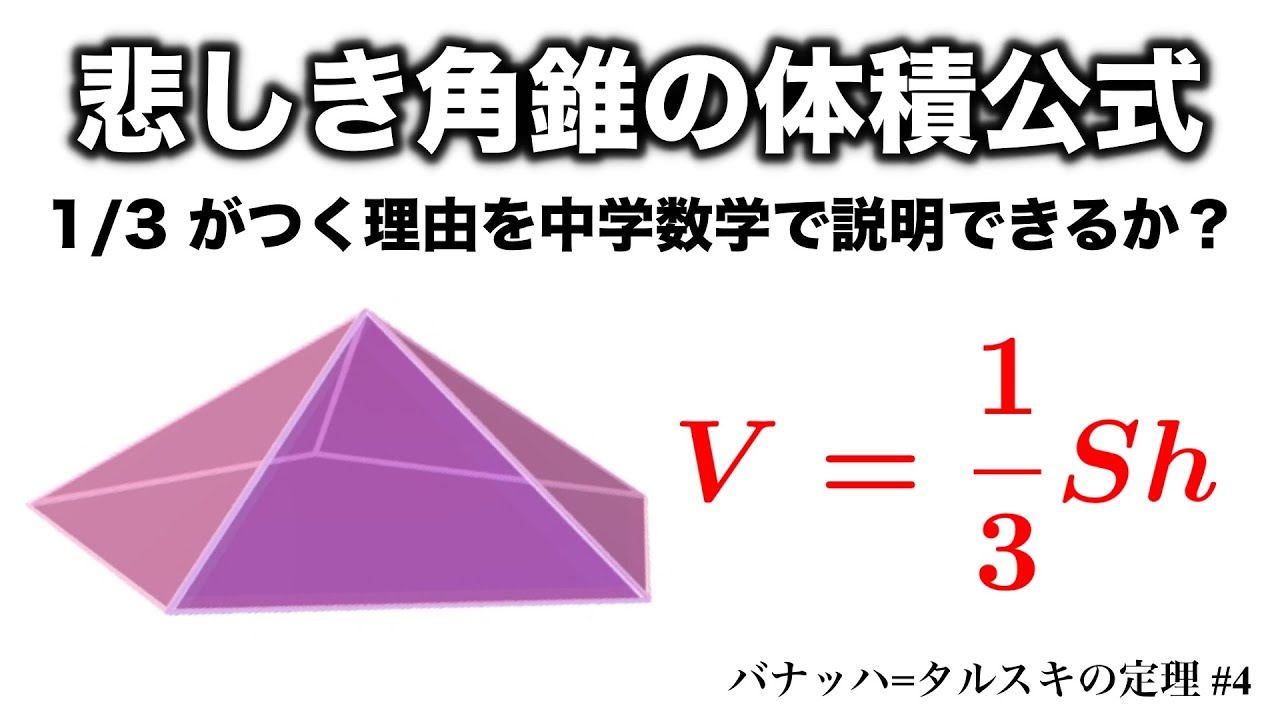1
1	1	1
1	1	1
1	1	1
1	1	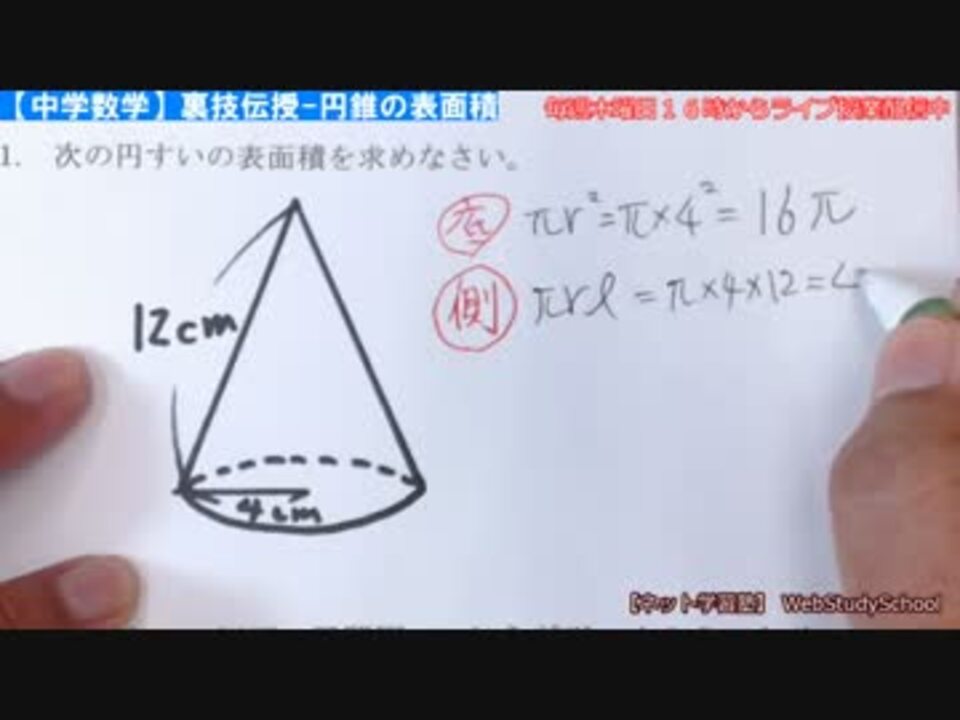1
1	1	1
1	1	1
1	1	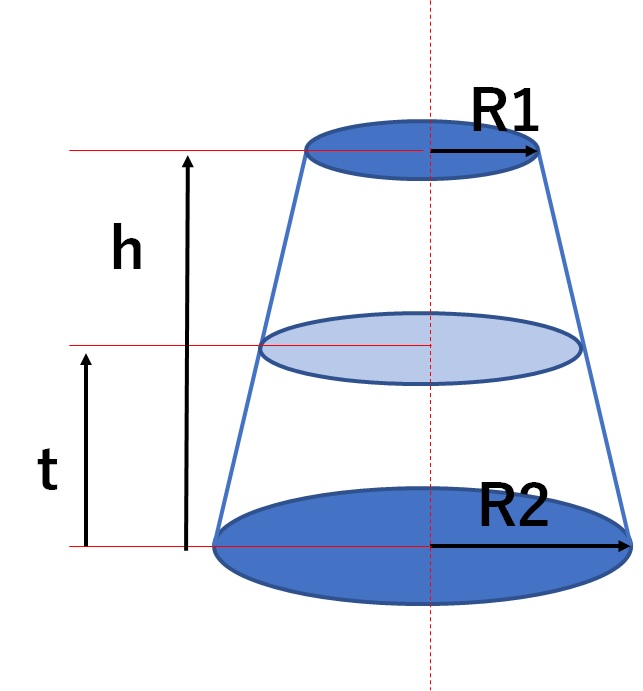1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	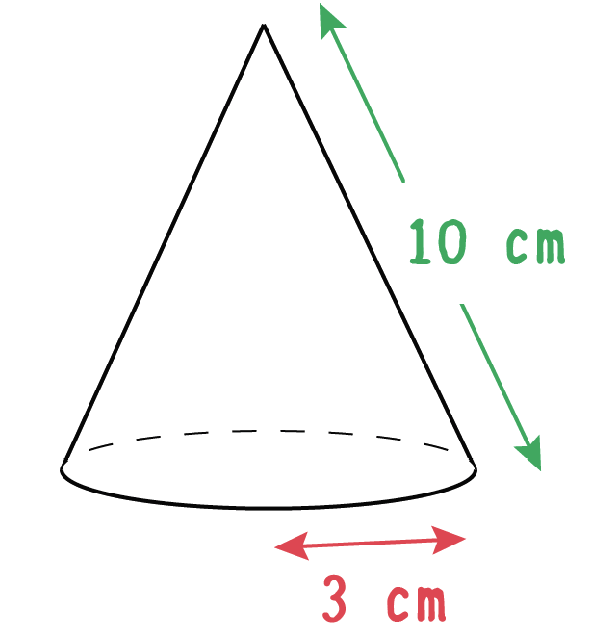1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1

 積分を用いて円錐の体積 を求める以下の公式を導出します． ここで， は底面の半径， は円錐の高さとします． 証明：まず，xy平面上に原点を通る直線を考えます．この直線とx軸とのなす角をθとすると，この直線は と表せます．この直線の式とx軸および2直線 および で囲まれた図形積分を用いた証明 二つ目の説明です。数学2の知識が必要になります。積分を使って V = 1 3 S h V=\dfrac{1}{3}Sh V = 3 1 S h を証明します。 底面積の形によらない（円錐でも三角錐でも四角錐でも適用可能）証明方法です。

Incoming Term: 円錐の体積 公式, 円錐の体積 公式 証明, 円錐の体積 公式 覚え方,